画像をダウンロード parabola congruent to y=x^2 320600

Axis\(y3)^2=8(x5) directrix\(x3)^2=(y1) parabolaequationcalculator y=3x^{2} en Related Symbolab blog posts Practice Makes Perfect Learning math takes practice, lots of practice Just like running, it takes practice and dedication If you wantY = 2 x2 4 x í 6 62/87,21 Graph the ordered pairs, and connect them to create a smooth curve The parabola extends to infinity The axis of symmetry is the line that goes through the vertex and divides the parabola into congruent halves It is located at x = ±2 Find the yinterceptConsider the parabola y = x 2 Since all parabolas are similar, this simple case represents all others Construction and definitions The point E is an arbitrary point on the parabola The focus is F, the vertex is A (the origin), and the line FA is the axis of symmetry The line EC is parallel to the axis of symmetry and intersects the x axis

Content Transformations Of The Parabola

Parabola congruent to y=x^2

Parabola congruent to y=x^2-Vertex\3x^22x5y6=0 vertex\x=y^2 vertex\ (y3)^2=8 (x5) vertex\ (x3)^2= (y1) parabolafunctionvertexcalculator enGet an answer for 'Write the equation of a parabola with a vertex of (2,3) that opens downward and is congruent to y=1/3x^2 ' and find homework help for other Math questions at eNotes

Find The Centroid Of The Area Bounded By The Parabola Y 4 X 2 And The X Axis Study Com

 y = a(x – h) 2 k, where (h, k) The axis of symmetry of a parabola is a vertical line that divides the parabola into two congruent halves The axis of symmetry always passes through the vertex of the parabola The x coordinate of the vertex is the equation of the axis of symmetry of the parabolaThanks so much in advance) Found 2 solutions by DrBeeee, josmiceliEach parabola is affine congruent to P 0 y 2 = x Each ellipse or circle is affine congruent to E 0 x 2 y 2 = 0 Each hyperbola is affine congruent to H 0 xy = 1 proof of theorem AC2 Since two curves which are affine congruent to the same curve are affine congruent, we see that the

 For example, when point P with coordinates (5,4) is reflecting across the Y axis and mapped onto point P', the coordinates of P' are (5,4)Notice that the ycoordinate for both points did not change, but the value of the xcoordinate changed from 5 to 5 You can think of reflections as a flip over a designated line of reflection Correct answer to the question Find the vertex of the parabola by completing the square x^26x8=y hmwhelpercomAnswer (1 of 4) The parabola has y axis as the axis Vertex is at V(0,0) The directrix y=2 is at distance 2 from the vertex V The Focus is at F=(0,2) Any point P(x,y) is at equidistance from y=2 and F PF^2=x^2(y2)^2 Distance from y=2 is y2 (y2)^2=x^2(y2)^2 y^22y4=x^2y^22y

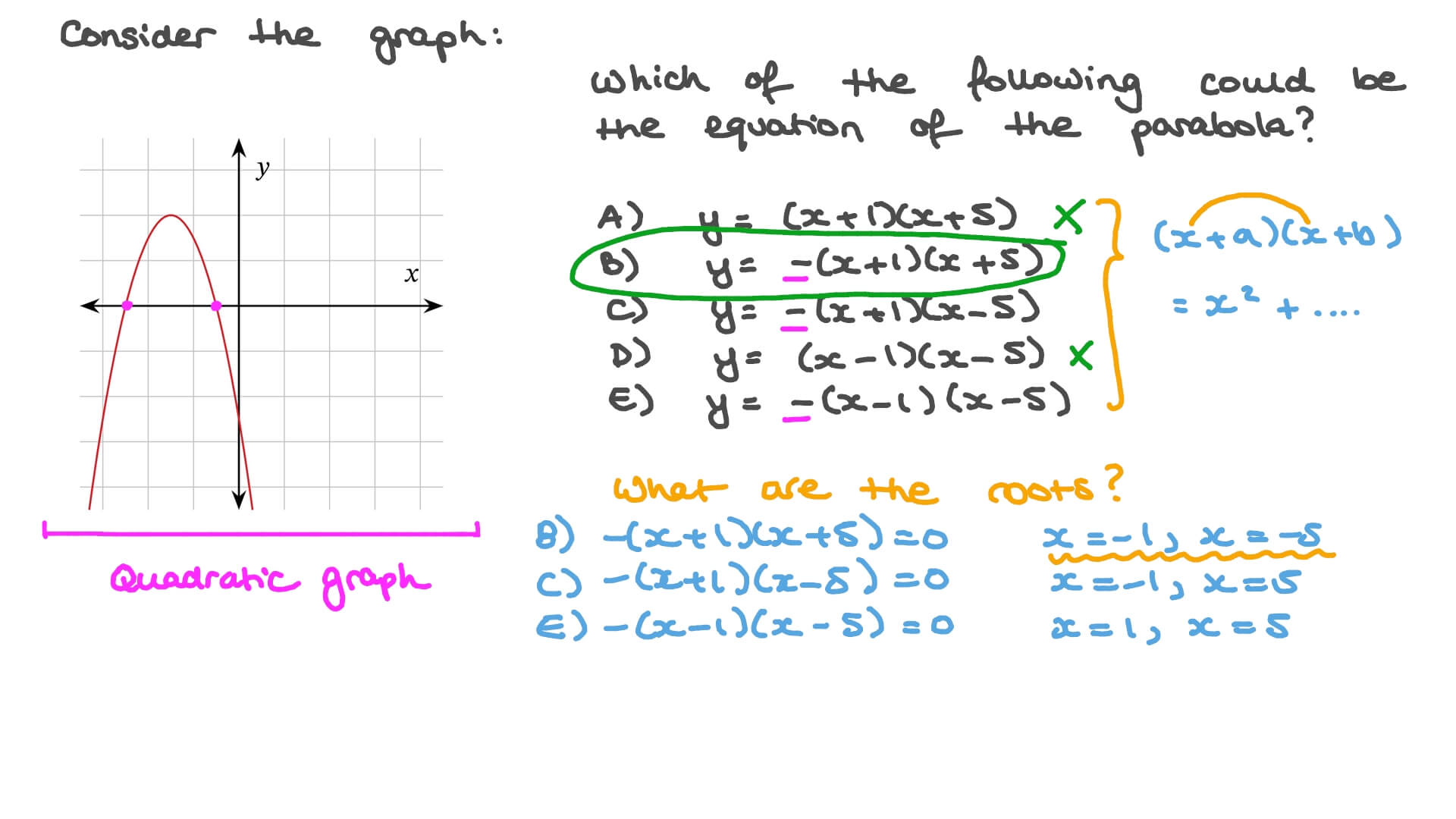
A parabola is congruent to y=x^2 and has xintercepts 1 and 5 determine the coordinates of the vertex Answer by Fombitz() ( Show Source ) You can put this solution on YOUR website!1 point 17) Which equation describes a parabola that opens downward, is congruent to y = x*2, and has its vertex at (0, 3)?Press J to jump to the feed Press question mark to learn the rest of the keyboard shortcuts You can't get any congruent triangles (which require three equal parts of a triangle to be equal), all you have are right angles as

Draw The Graphs Of Following Quadratic Functions I Y X 2 X 1 Ii Y X 2 2x 3 Iii Y 2 X X 2 Iv Y X 1 X 2

Content Transformations Of The Parabola

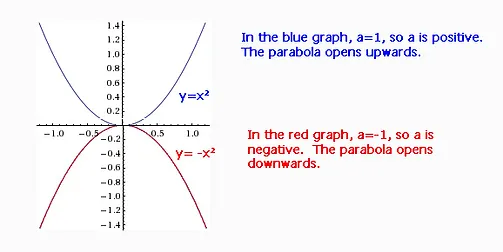
 Consider a parabola P that is congruent to y=x^2, opens upward,and has its vertex at (2,4) Now find the equation of a new parabola that results ifTo find the endpoints, substitute x = 6 x = 6 into the original equation ( 6, ± 12) ( 6, ± 12) Next we plot the focus, directrix, and latus rectum, and draw a smooth curve to form the parabola Figure 7 Try It Graph y2 =−16x y 2 = − 16 x Identify and labelThe equation of a parabola can be converted into the vertex form y = a(xh) 2 k, where h = xcoordinate of vertex, and k = ycoordinate of vertex Also, if a is positive, the parabola opens upward Also, if a is positive, the parabola opens upward

What Is The Equation Of A Parabola That Opens Upward And Has X Intercepts At 2 0 And 6 0 Homeworklib

Vertical Shifts Of Quadratic Functions Ck 12 Foundation

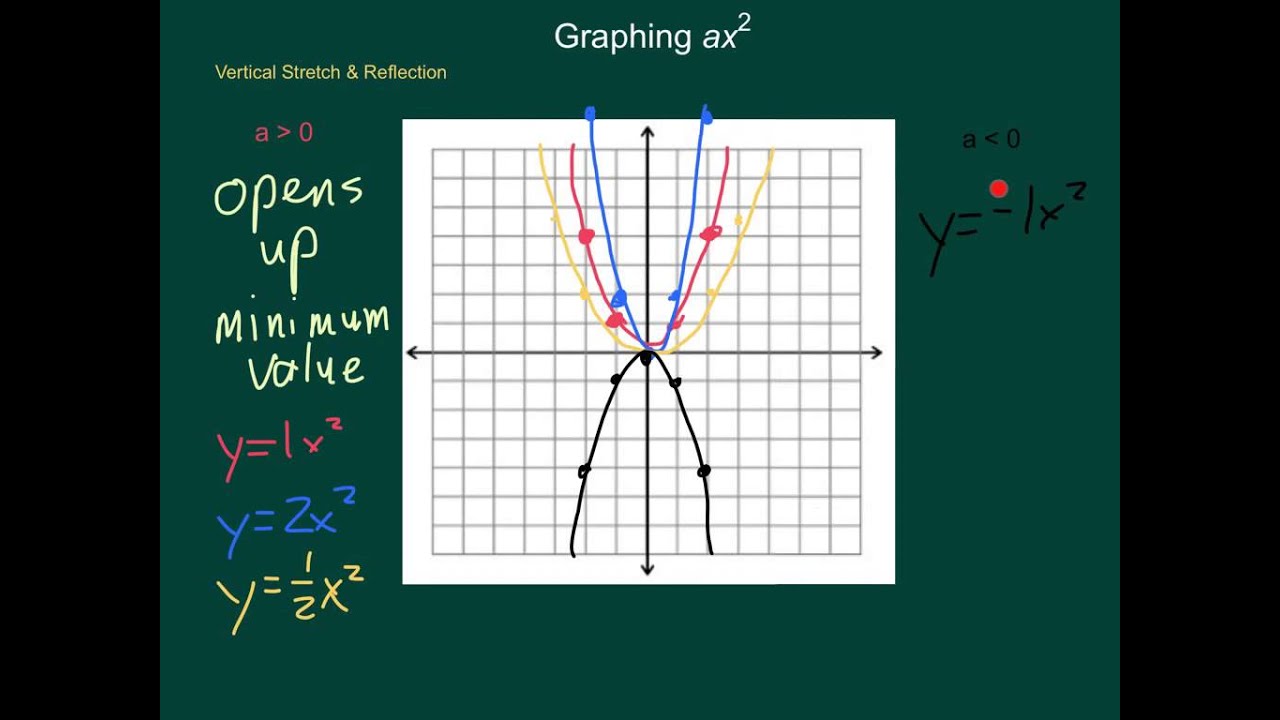
 Parabola described by y=2x^2 is narrower than the parabola described by y=x^2 Parabola described by y=2x^2 is narrower than the parabola described by y=x^2 Smaller the coefficient of x^2 wider the curveWhat is the maximum vertical distance between the line y = x 6 and the parabola y = x2 for −2 ≤ x ≤ 3?Write the equation for each parabola with the given information mark each a) Congruent to y = 2x opens up, with a vertex of (51) > Congruent to y =(x 2), maximum vukue of 4, equation of asis of symmetry * = 2 10 Write the equation of the parabola with given vertex, if it passes through the given pointcz a) vertex (0,1), passing through (29) b)

Transformations Of Functions Ck 12 Foundation

Question Video Equations Of Parabolic Curves Nagwa

The equation of this new parabola is thus y = x 2 9 The vertex of this parabola is now (0, 9), but it has the same axis of symmetry Similarly, the basic parabola becomes y = x 2 − 9 when translated down 9 units, with vertex (0, 9) We can confirm this In δabc shown below, ∠bac is congruent to ∠bca triangle abc, where angles a and c are congruent given base ∠bac and ∠acb are congruent prove δabc is an isosceles triangle when completed (fill in the blanks), the following paragraph proves that line segment ab is congruent to line segment bc making δabc an isosceles triangleSince it is so simple to find the yintercept (and it will probably be a point in my Tchart anyway), they are only asking for the xintercepts this timeTo find the xintercept, I set y equal 0 and solve

Shifting Parabolas Video Khan Academy

Algebra1 Graphing Y Ax 2 Youtube

The set of points (x, y) whose distance from the line y = 2 x 2 is the same as the distance from (2, 0) is a parabola This parabola is congruent to the parabola in standard form y = K x 2 for some K which is equal toArrow_forward Question Write an equation for a parabola that is congruent to the graph of y = x 2, opens downward, and has its vertex at (3,1) check_circle Expert AnswerTherefore the "p" translates the parabola horizontally across the xaxis, and the "q" translates the parabola vertically across the yaxis The "p" value also represents our axis of symmetry, the line that divides the graph into two congruent parts, so that the graph on one side is the mirror image of the graph on the other side

Parabola Wikipedia

Parabola Parent Function Mathbitsnotebook A1 Ccss Math

Generally, only the higher level of high school maths contain locus questions (especially year 11) As discussed earlier, we have to deal with the locus form of quadratics, which is given as $$(xh)^2=±4a(yk)$$ We have already seen that (h,k) represent the vertex of the quadraticFirst week only $499!Answer to 1 point 17) Which equation describes a parabola that Math;

Find The Centroid Of The Area Bounded By The Parabola Y 4 X 2 And The X Axis Study Com

Quadratic Function

Y = − x 2 y = x 2 y = − x 2 y = x 2 Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k a = − 1 a = 1 h = 0 h = 0 k = 0 k = 0 Since the value of a a is negative, the parabola opens down Opens Down Find the vertex ( h, k) ( h, k)Y = (x 3)2 1 y = – x2 3 B) y = (x – 3)2 y = x2 3Suppose the parabola with equation y = 2x^2 undergoes the translation T2,3 Find an equation for its image Vertex form is y k = a(x h)^2 Also given is Th,k, with h = 2 and k = 3 Also given is that a = 2 in the expression 2x^2 Now fill in a, h and k with the given numbers y 3 = 2(x 2)^2 > and there's the answer

Example 1 Write A Quadratic Function In Vertex Form Write A Quadratic Function For The Parabola Shown Solution Use Ver Quadratics Quadratic Functions Parabola

Parabola Sketching Y 2x 2 4x 6 From The Parabola Translation Download Scientific Diagram

 Six congruent copies of the parabola $y = x^2$ are arranged in the plane so that each vertex is tangent to a circle, and each parabola is So p = 2 , q = 3 Given that congruent to y= 2x² and opens down congruent means has the same a value (same shape) of y= 2x² So a = 2, But it opens downSo a = 2 Substitute a = 2 , p = 2 , q = 3 in vortex form y = (2)(x (2))² 3 y = 2(x 2)² 3 The solution is y = 2(x 2)² 31) a rotation of 90 degrees counterclockwise about the origin 2) a translation of three units to the left and three units up 3) a rotation of 180 degrees about the origin 4) a reflection over the line y =x

Parabola Parent Function Mathbitsnotebook A1 Ccss Math

Quadratic Functions Academic Support Center

If your parabola only crosses the xaxis at a single point, a, then that point will be the vertex of the parabola The equation of such a parabola will be mathy=(xa)^2/mathParabola congruent to y = ax2 xintercepts at x = m and x = n (aka the "zeros" of the quadratic function) Regardless of the form, a parabola opens up when a > 0 and opens down when a < 0, with the axis of symmetry passing through the vertex of the parabolaSubstitute the values of a a, d d, and e e into the vertex form a ( x d) 2 e a ( x d) 2 e 4 x 2 4 x 2 4 x 2 4 x 2 Set y y equal to the new right side y = 4 x 2 y = 4 x 2 y = 4 x 2 y = 4 x 2 Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k

Engageny Org

Solved Write An Equation Of A Parabola That Has A Vertex 3 8 Opens Downward And I Congruent In Shape To The Graph Of Y 5x2 1 The X Interce Course Hero

Every parabola has an axis of symmetry which is the line that divides the graph into two perfect halves On this page, we will practice drawing the axis on a graph, learning the formula, stating the equation of the axis of symmetry when we know the parabola's equation11 The graph below shows two congruent triangles, ABC and A'B'C' Which rigid motion would map ABC onto A'B'C'? Consider a parabola P that is congruent (has the same shape) to y=x^2 , opens upward, and has vertex (2,3) Now find the equation of a new parabola that results if P is Compressed to a factor of 1/2 Translated 2 units to the left Translated 3 units up Reflected in the xaxis and translated 2 units to the right and 4 units down

How Do You Graph Y X 2 2

Consider A Parabola Math Y X 2 Math The Line That Goes Through The Point 0 3 2 And Is Orthogonal To A Tangent Line To The Part Of Parabola Math Y X 2 Math With Math X 0 Math Is Math Y Ax 3 2 Math What

Find the xintercepts and vertex of y = –x 2 – 4x 2;•Consider a parabola that is congruent to y = 2 x, and with vertex (2, ‐4) Find the equation of a new parabola that results if it is (a) Translated 6 units down (b) Translated 5 units left (c) Translated 6 units up and 5 units rightWe can find the parabola's equation in vertex form following two steps Step 1 use the (known) coordinates of the vertex, ( h, k), to write the parabola 's equation in the form y = a ( x − h) 2 k the problem now only consists of having to find the value of the coefficient a Step 2 find the value of the coefficient a by substituting

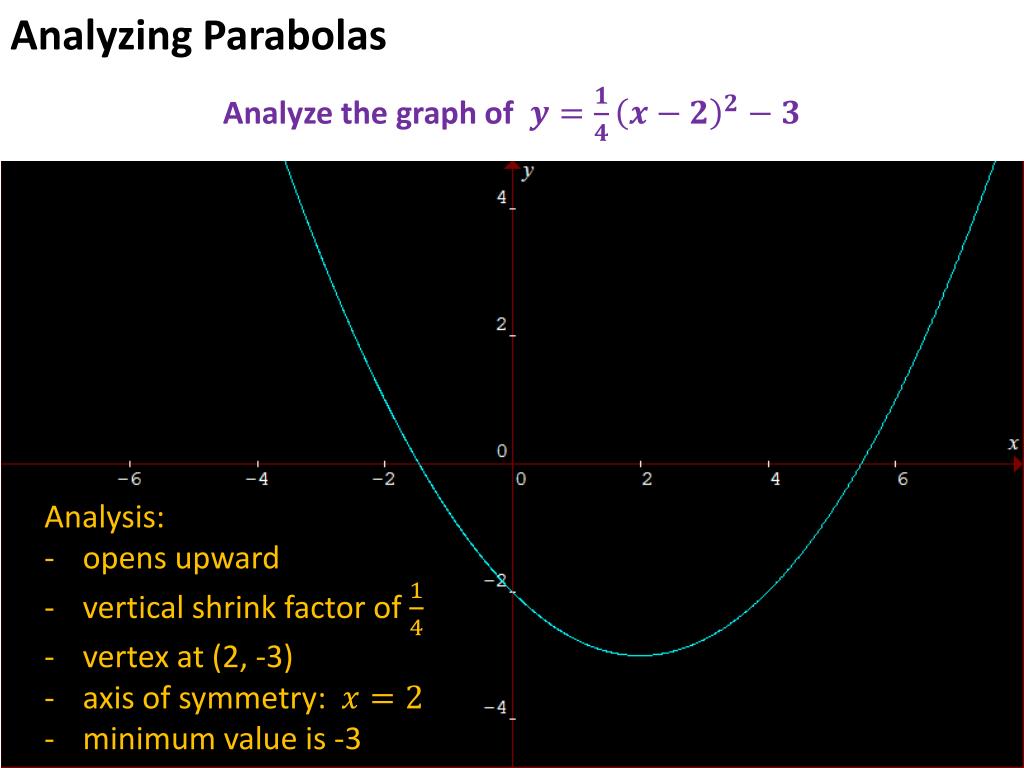
Ppt Analyzing Parabolas Powerpoint Presentation Free Download Id

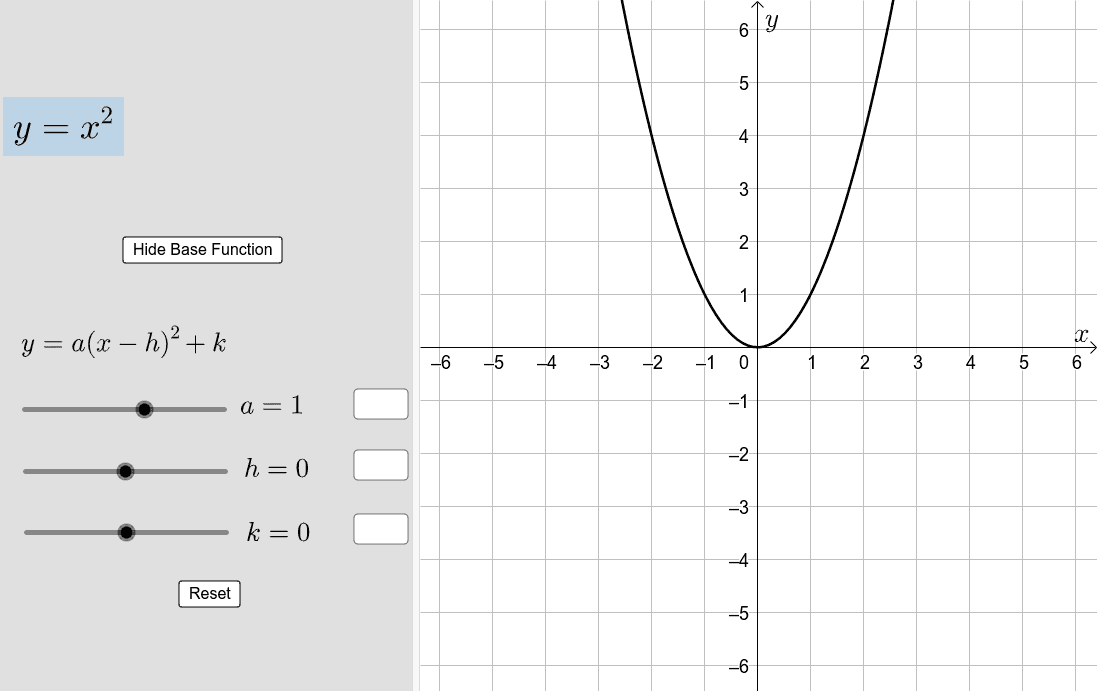
Transforming The Graph Of Y X Geogebra

1 start by plotting the vertex (if the parabola is congruent to y=x(squared) 2 plot the second point by moving left one unit and up one unit from the last point 3 plot the third point by moving left one unit and up three units from the last point 4 plot mirrored points to get the right half of the parabolaWrite the equation with y 0 on one side y 0 = x 0 2 4 − x 0 5 This equation in ( x 0, y 0) is true for all other values on the parabola and hence we can rewrite with ( x, y) So, the equation of the parabola with focus ( 2, 5) and directrix is y = 3 is y = x 2 4 − x 5Answer Correct option is B y = 0 The axis of symmetry of a parabola is a vertical line that divides the parabola into two congruent halves y2 2x = 0 y2 = −2x is the equation of a parabola It is in the form of y2 = 4ax So axis of parabola will be xaxis ( y = 0) as shown in the given figure Answer verified by Toppr

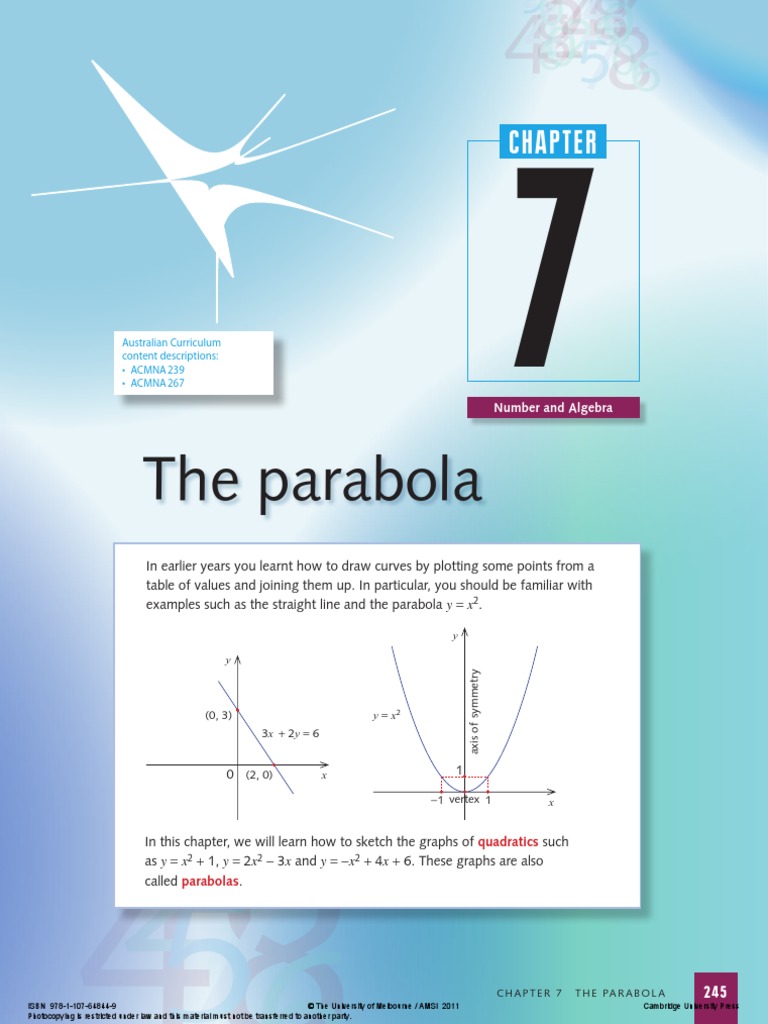
Chap 7 The Parabola Pdf Pdf Quadratic Equation Geometry

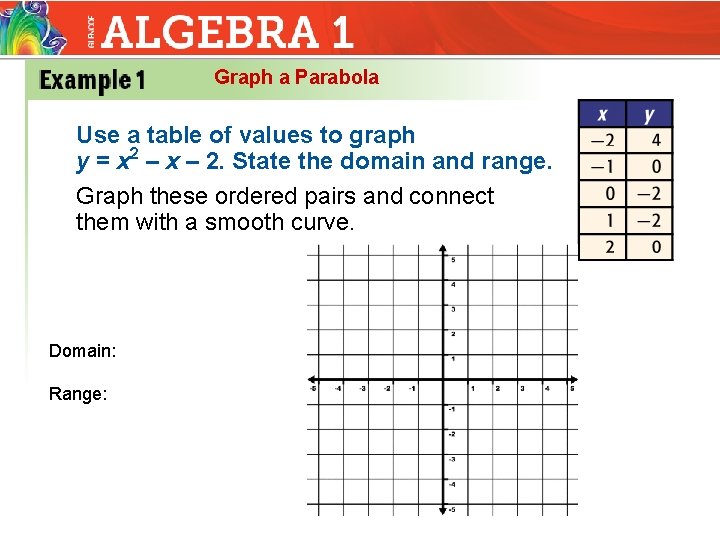
9 1 Identifying The Characteristics Of And Graphing

Parabolic mirrors concentrate incoming vertical light beams in their focus We show this Consider in figure 2 the arbitrary vertical light beam B (blue, parallel to the yaxis) that enters the parabola and hits it at point P = (x 1, y 1)The parabola (red) has focus in point FThe incoming beam is reflected at P obeying the wellknown law incidence angle is equal to angle of reflectionWrite an equation for a parabola that is congruent to the graph of y = x2, opens downward, and has its vertex at (3,1) close Start your trial now!Y=x2–3 and compare it to † y=(x3)2 The analysis of responses attended to (1) common trends in explanations, and (2) attitudes towards perceived inconsistency RESULTS The fact that the shape of † y=(x3)2is a parabola that is congruent to the canonical parabola y=x2 was taken for granted by teachers and students alike The fact that the

1

Quadratic Equation Congruent To Parabola Pass Through Point With Y Intercept As Another Curve Youtube

Use traces to sketch the surface z = 4x2 y2 Solution If we put x = 0, we get z = y2, so the yzplane intersects the surface in a parabola If we put x = k (a constant), we get z = y2 4k2 This means that if we slice the graph with any plane parallel to the yzplane, we obtain a parabola that opens upward Similarly, if y = k, 2the trace is z = 4x k2, which is again a parabola that opensView HW Day 2 congruent parabolas (1)pdf from MATH 1101 at Syosset High School Name _ Day 2 – congruent parabolas 1) Write the equation of the parabola whose directrix is x = 2Question Find the equation of the parabola with vertex (4,4), the parabola opens upwards and is congruent to y=1/2x^2 Can you please help me?

Exploration Of Parabolas

Graphing Quadratic Functions Lesson Article Khan Academy

About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsAdvanced Math questions and answers;

Consider The Parabola Whose Equation Is Y X 2 4x And The Line Y 2x B Then Whichfollowing Is Are Correct

Exploration Of Parabolas

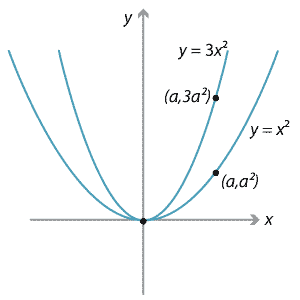
Content Transformations Of The Parabola

Consider A Parabola P That Is Congruent To Y X 2 Opens Upward And Has Vertex 0 0 Find The Brainly Com

Graphing Quadratic Functions

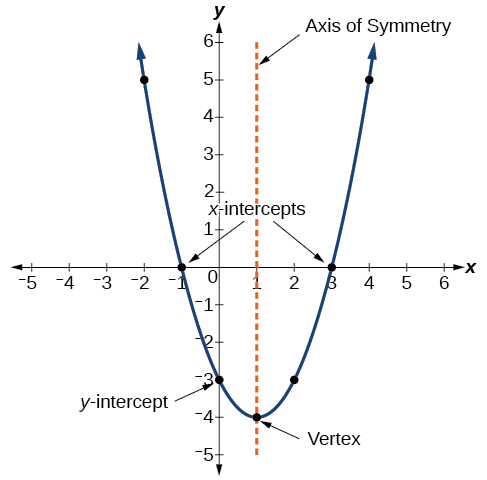
5 2 Quadratic Functions Mathematics Libretexts

Plot A Graph For The Equation Y X 2 4x 1

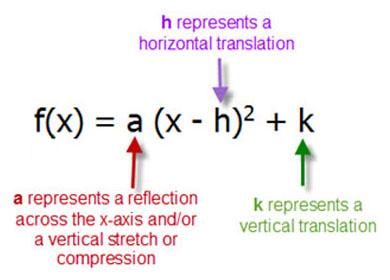
Untitled Document

Find The Centroid Of The Region Bounded By The Parabola Y X 2 The Line X 2 And The X Axis Study Com

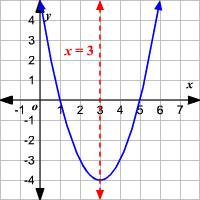
Axis Of Symmetry Of A Parabola

The Parabola

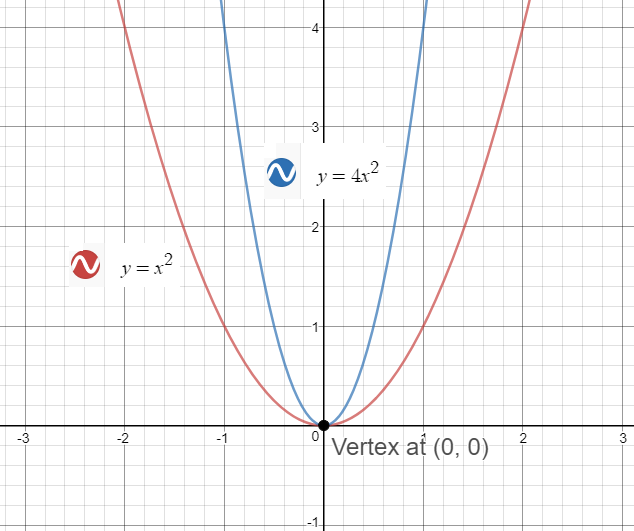
How To Graph A Parabola Y 4x 2 Socratic

Draw The Graphs Of Following Quadratic Functions I Y X 2 X 1 Ii Y X 2 2x 3 Iii Y 2 X X 2 Iv Y X 1 X 2

Content Transformations Of The Parabola

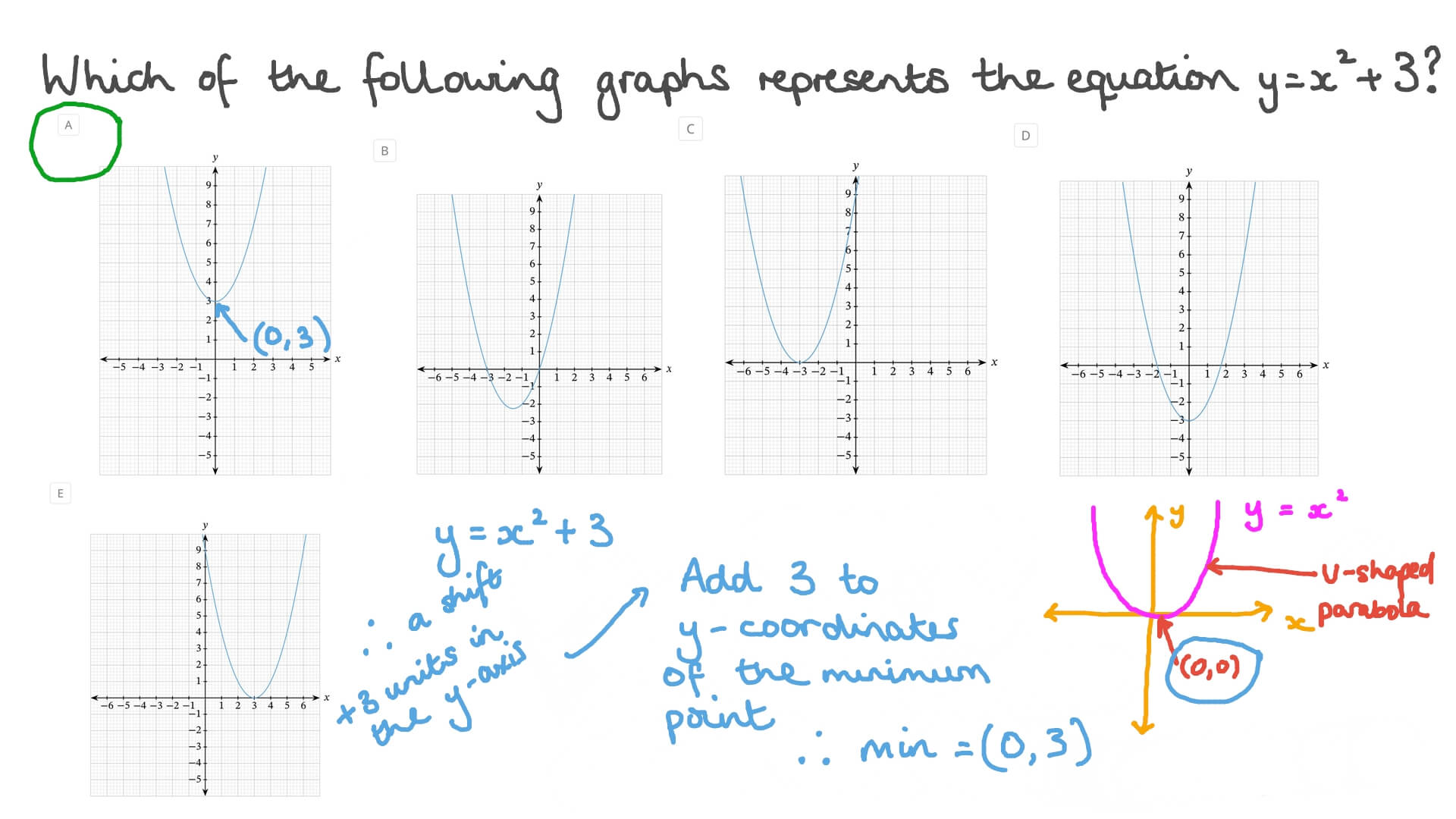
Question Video Identifying Graphs Of Quadratic Equations In Vertex Form Nagwa

Content Transformations Of The Parabola

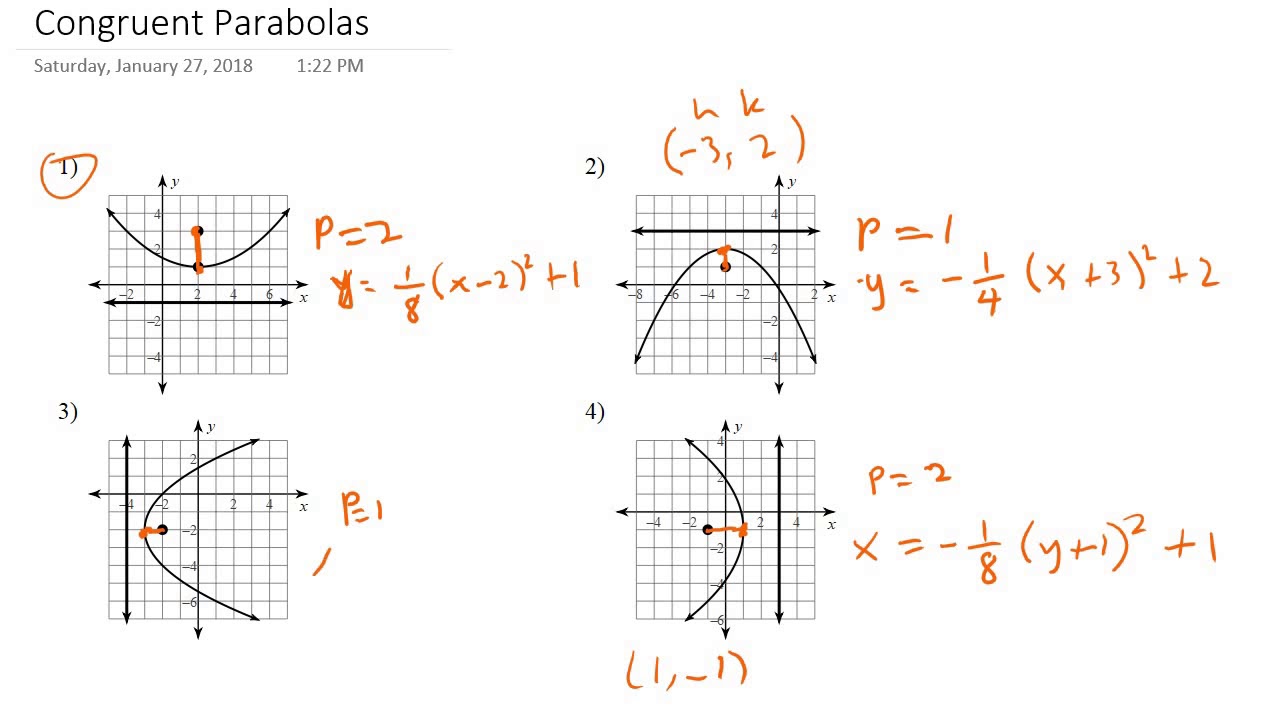
Congruent Parabolas Youtube

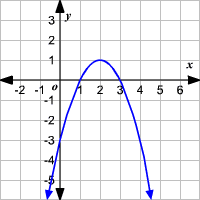
Axis Of Symmetry Of A Parabola

L2d2ii Html

Solved Write The Equation Of The Parabola That Opens Down Has A Vertex V 1 5 And Is Congruent To Y I332 Answer In The Form 3 A C H 2 I Course Hero

The Axis Of A Parabola Is Along The Line Y X And The Distance Of Its Vertex And Focus From The Origin Are Sqrt 2 And 2sqrt 2 Respectively If Vertex And Focus Both

Algebra Ii Module 1 Topic C Lesson 35 Student Version

Whiteplainspublicschools Org

Solution Find The Equation Of The Parabola With Vertex 4 4 The Parabola Opens Upwards And Is Congruent To Y 1 2x 2 Can You Please Help Me Thanks So Much In Advance

Pubs Lib Umn Edu

In The Figure Below The Equation Of The Solid Parabola Is Y X 2 21 And The Equation Of The Line Is Y x Determine The Area Of The Shaded Region Set Up The Integral That

Solved 1 Point 17 Which Equation Describes A Parabola That Chegg Com

Vertex Form Chapter 4 Quad Relationships

Quadratic Functions Academic Support Center

Attributes Of Quadratic Flashcards Quizlet

Solution Can You Help Me With This Problem A Parabola Is Congruent To Y X 2 And Has X Intercepts 1 And 5 Determine The Coordinates Of The Vertex

Algebra 2 Module 1 Lesson 35 Video Youtube

Solving Quadratic Equations By Graphing Examples

Content Transformations Of The Parabola

The Parabola Shown Is Congruent To Y X 2 A What Are The Zeroes Of The Function B Write The Equation In Factored Form Quora

Scaling Reflecting Parabolas Video Khan Academy

How To Find The Minimum Or Maximum Value Of A Function In Vertex Form

What Are The X Intercepts And The Coordinates Of The Vertex For The Parabola Y X 2 4x 12 Quora

Lesson 4 2 Graphing Parabolas Using Transformations Ppt Download

1

What Is The Equation For A Parabola That Is Congruent To The Graph Of Y X Squared Opens Downward And Has Its Vertex At 3 1 Quora

Engageny Org

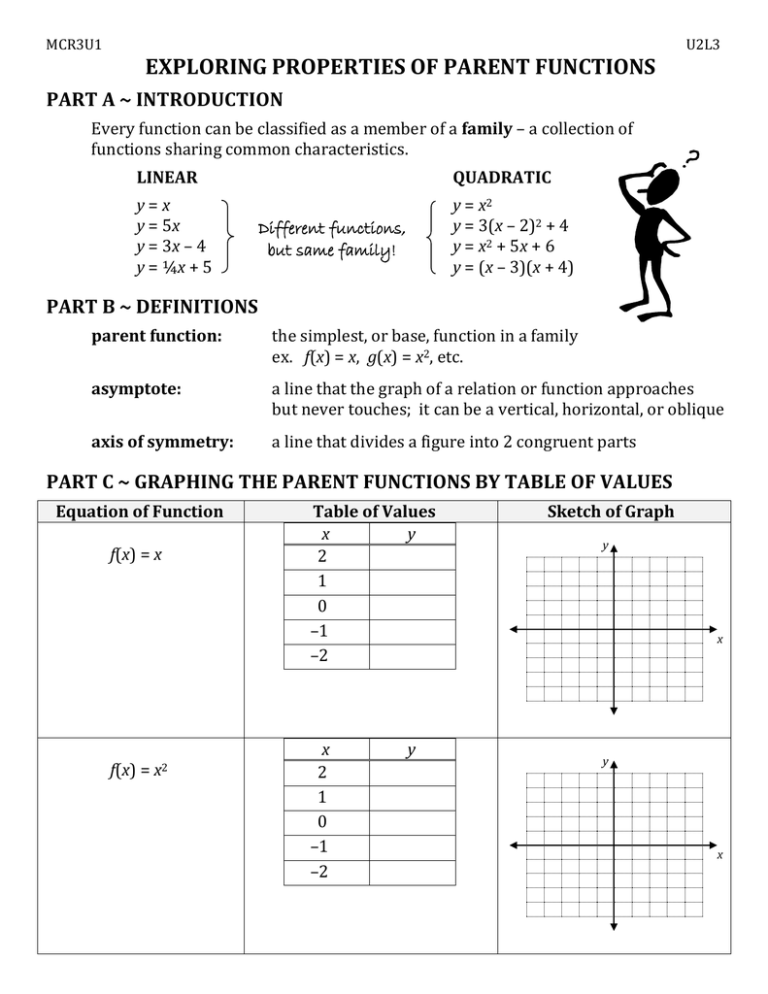
Exploring Properties Of Parent Functions Part A Introduction

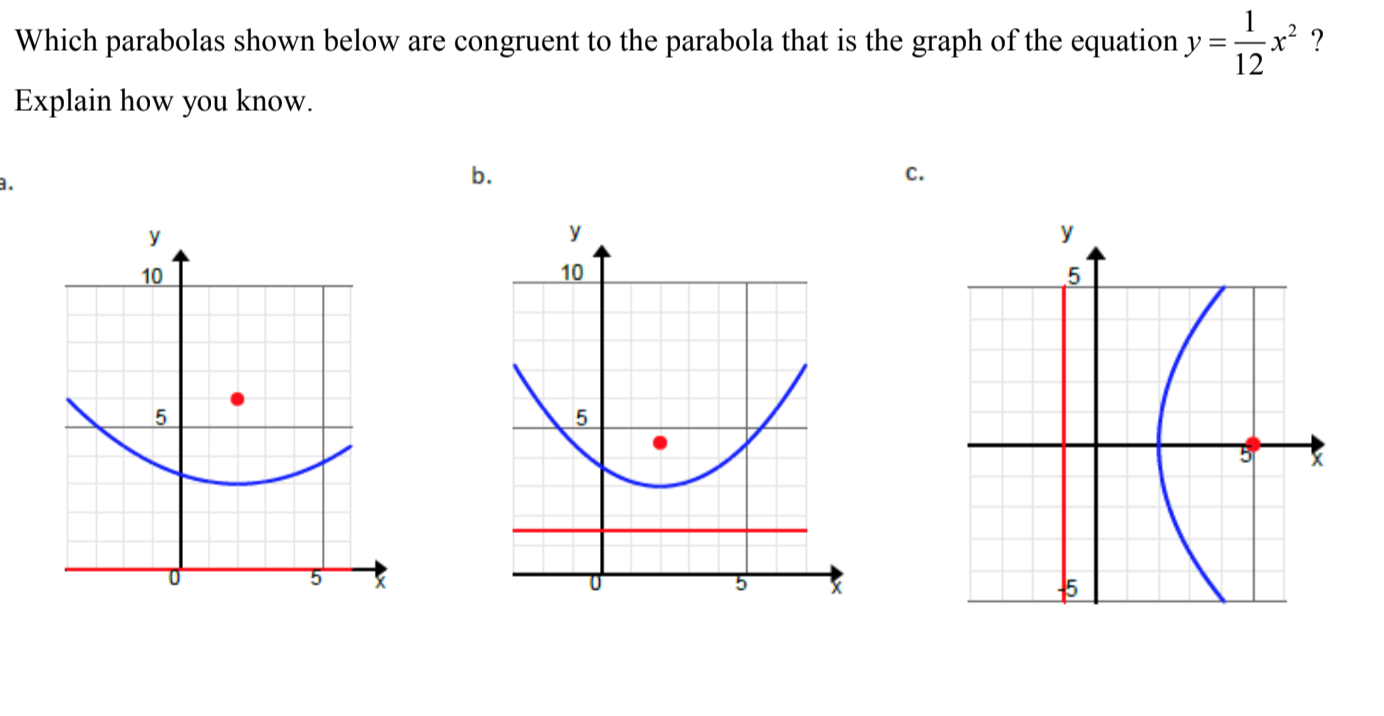
Solved Which Parabolas Shown Below Are Congruent To The Chegg Com

The Graph Of Y X2 6x 9 Is Shown Below What Is The Solution Set For Brainly Com

Transformations Of Functions Ck 12 Foundation

1

Chapter 4 Quadratics 4 3 Using Technology To Investigate Transformations Ppt Download

Math Spoken Here Classes Quadratic Equations 3

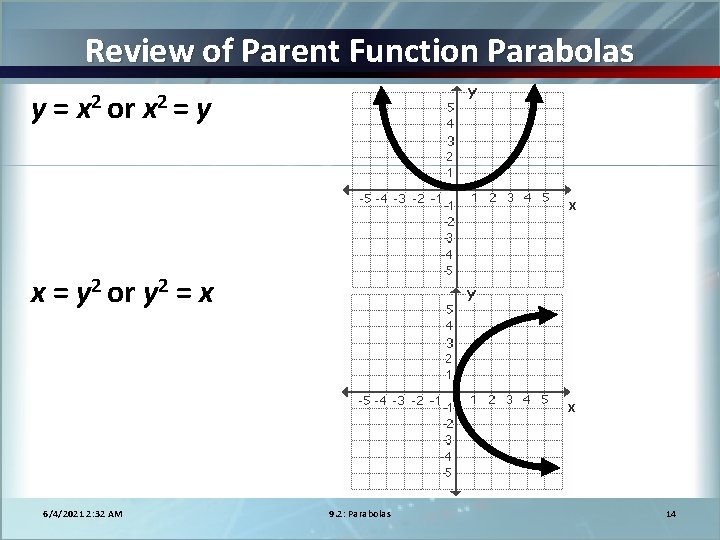
Worksheet Key 6421 2 32 Am 9 2

Chapter 4 Quadratics 4 3 Using Technology To Investigate Transformations Ppt Download

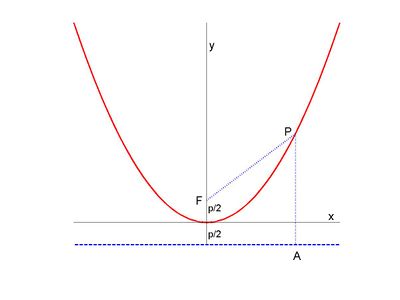
Parabola Knowino

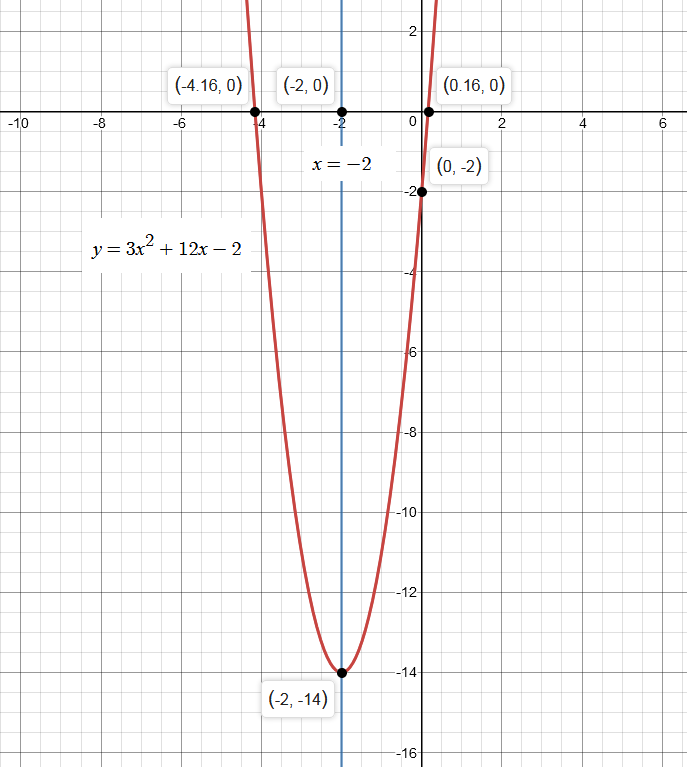
What Is The Axis Of Symmetry And Vertex For The Graph Y 3x 2 12x 2 Socratic

Axis Of Symmetry Of A Parabola

Blessedmotherteresa Typepad Com

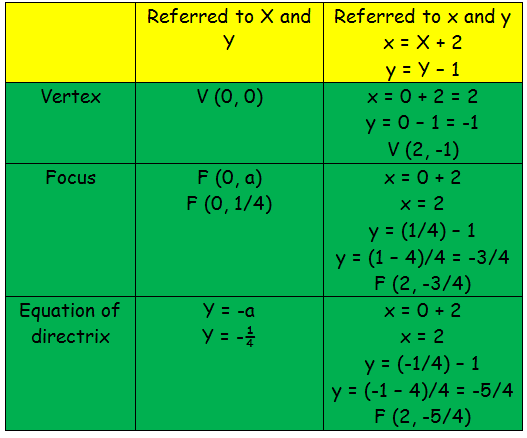
How To Find Focus Directrix And Vertex Of Parabola

Solved Determine A Possible Equation For Each Parabola On Chegg Com

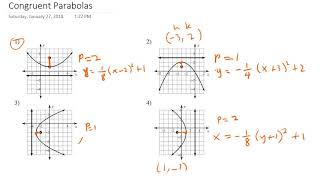
Congruent Parabolas Youtube

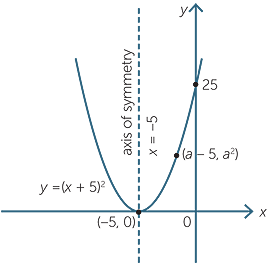
Quadratic Function

Parabola Wikipedia

What Is The Equation For A Parabola That Is Congruent To The Graph Of Y X Squared Opens Downward And Has Its Vertex At 3 1 Quora

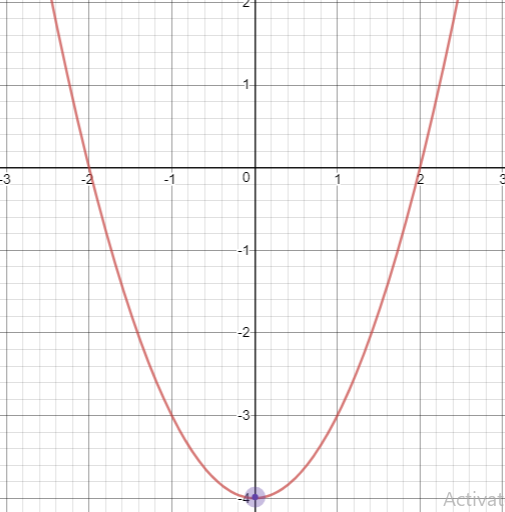
Solving Quadratic Equations By Graphing

Solved 2 Marks 4 If The Point 2 7 Is On The Parabola Y Chegg Com

L2d2ii Html

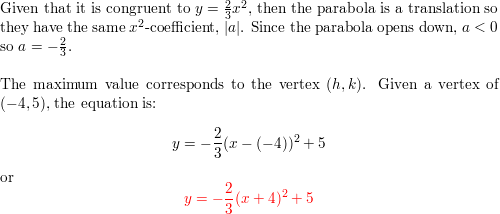
Write The Equation For Each Parabola In The Form Y A X H 2 K With The Given Information Congruent To Y 2 3x 2 Opens Down And Has A Maximum Value At 4 5 Homework Help And

Blessedmotherteresa Typepad Com

Graphs Of Parabolas Vertex Form Pdf

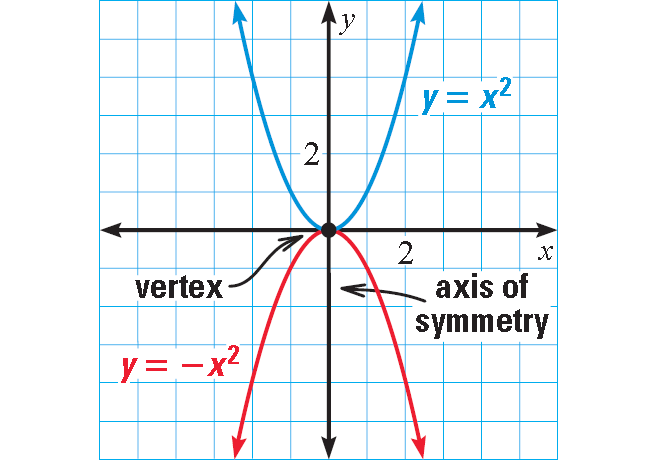
Graphing Quadratic Functions Parabola

The Point 5 4 Lies On The Graph Of A Quadratic Function Whose Axis Of Symmetry Is X 2 What Is Another Point On The Graph Quora

Ppt Translating And The Quadratic Family Powerpoint Presentation Free Download Id

1

Unique Quadratic Equation In The Form Y Ax 2 Bx C

Quadratic Function

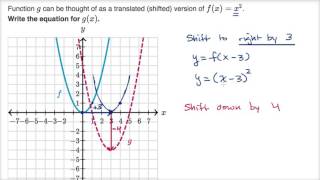
Shifting Parabolas Video Khan Academy

Resourceaholic Tricks And Tips 3 Quadratics

What Is The Equation For A Parabola That Is Congruent To The Graph Of Y X Squared Opens Downward And Has Its Vertex At 3 1 Quora